Page 29 - Chip Scale Review_November December_2021-digital

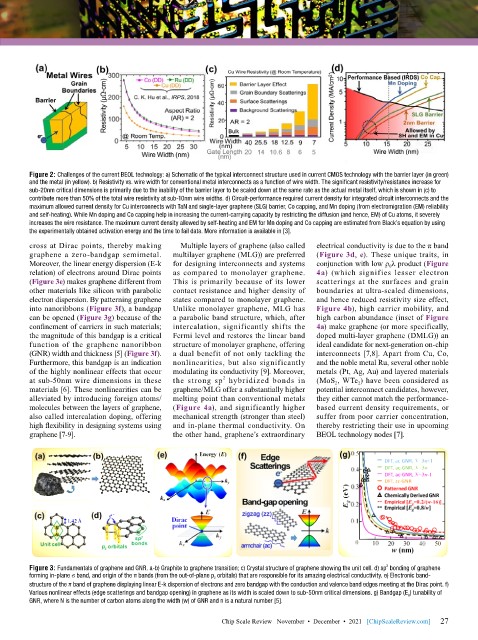
Figure 2: Challenges of the current BEOL technology: a) Schematic of the typical interconnect structure used in current CMOS technology with the barrier layer (in green)
and the metal (in yellow). b) Resistivity vs. wire width for conventional metal interconnects as a function of wire width. The significant resistivity/resistance increase for
sub-20nm critical dimensions is primarily due to the inability of the barrier layer to be scaled down at the same rate as the actual metal itself, which is shown in (c) to
contribute more than 50% of the total wire resistivity at sub-10nm wire widths. d) Circuit-performance required current density for integrated circuit interconnects and the
maximum allowed current density for Cu interconnects with TaN and single-layer graphene (SLG) barrier, Co capping, and Mn doping (from electromigration (EM) reliability
and self-heating). While Mn doping and Co capping help in increasing the current-carrying capacity by restricting the diffusion (and hence, EM) of Cu atoms, it severely
increases the wire resistance. The maximum current density allowed by self-heating and EM for Mn doping and Co capping are estimated from Black’s equation by using
the experimentally obtained activation energy and the time to fail data. More information is available in [3].
cross at Dirac points, thereby making Multiple layers of graphene (also called electrical conductivity is due to the π band
graphene a zero-bandgap semimetal. multilayer graphene (MLG)) are preferred (Figure 3d, e). These unique traits, in
Moreover, the linear energy dispersion (E-k for designing interconnects and systems conjunction with low ρ 0 λ product (Figure
relation) of electrons around Dirac points as compared to monolayer graphene. 4a) (which signifies lesser electron
(Figure 3e) makes graphene different from This is primarily because of its lower scatterings at the surfaces and grain
other materials like silicon with parabolic contact resistance and higher density of boundaries at ultra-scaled dimensions,
electron dispersion. By patterning graphene states compared to monolayer graphene. and hence reduced resistivity size effect,
into nanoribbons (Figure 3f), a bandgap Unlike monolayer graphene, MLG has Figure 4b), high carrier mobility, and
can be opened (Figure 3g) because of the a parabolic band structure, which, after high carbon abundance (inset of Figure
confinement of carriers in such materials; intercalation, significantly shifts the 4a) make graphene (or more specifically,
the magnitude of this bandgap is a critical Fermi level and restores the linear band doped multi-layer graphene (DMLG)) an
function of the graphene nanoribbon structure of monolayer graphene, offering ideal candidate for next-generation on-chip
(GNR) width and thickness [5] (Figure 3f). a dual benefit of not only tackling the interconnects [7,8]. Apart from Cu, Co,
Furthermore, this bandgap is an indication nonlinearities, but also significantly and the noble metal Ru, several other noble
of the highly nonlinear effects that occur modulating its conductivity [9]. Moreover, metals (Pt, Ag, Au) and layered materials
2
at sub-50nm wire dimensions in these the strong sp hybridized bonds in (MoS 2 , WTe 2 ) have been considered as
materials [6]. These nonlinearities can be graphene/MLG offer a substantially higher potential interconnect candidates, however,
alleviated by introducing foreign atoms/ melting point than conventional metals they either cannot match the performance-
molecules between the layers of graphene, (Figure 4a), and significantly higher based current density requirements, or
also called intercalation doping, offering mechanical strength (stronger than steel) suffer from poor carrier concentration,
high flexibility in designing systems using and in-plane thermal conductivity. On thereby restricting their use in upcoming
graphene [7-9]. the other hand, graphene’s extraordinary BEOL technology nodes [7].

2
Figure 3: Fundamentals of graphene and GNR. a-b) Graphite to graphene transition; c) Crystal structure of graphene showing the unit cell. d) sp bonding of graphene
forming in-plane σ band, and origin of the π bands (from the out-of-plane p z orbitals) that are responsible for its amazing electrical conductivity. e) Electronic band-
structure of the π band of graphene displaying linear E-k dispersion of electrons and zero bandgap with the conduction and valence band edges meeting at the Dirac point. f)
Various nonlinear effects (edge scatterings and bandgap opening) in graphene as its width is scaled down to sub-50nm critical dimensions. g) Bandgap (E g ) tunability of
GNR, where N is the number of carbon atoms along the width (w) of GNR and n is a natural number [5].

27
Chip Scale Review November • December • 2021 [ChipScaleReview.com] 27