Page 23 - ChipScale_Jan-Feb_2020-digital

Wavefront phase imaging for global and local

wafer geometry

By Juan M. Trujillo-Sevilla, Jose M. Ramos-Rodríguez, Jan Gaudestad [Wooptix]
W avefront phase imaging Introduction on a surface keeping its angle with respect

( W F P I ) i s a n e w
T h e ge o m e t r y of u n p a t t e r n e d
technique to measure silicon wafers used as substrates for IC to the surface normal. The reflected beam
will carry the wavefront phase, where the
wafer geometry on a full wafer in a manufacturing is critical for process value is proportional to the surface height
single image snapshot providing depth control and ultimately, for device yield. map. In our case, we are using a collimated
information for every pixel. The number of Wafer geometry has many characteristics red (λ = 650nm) light beam that reflects
topography data points for the entire wafer that have been classified based on spatial onto the surface—the reflection angle of
will be proportional to the number of pixels wavelength (λs) and amplitude (Z height each ray is exactly two times the angle of
in the image sensor, allowing for millions resolution) (Figure 1) [2]. Nanotopography the surface normal [4].
of data points to be acquired in less than a (NT) is defined as height variations with There exists a value that defines the
second. Sub-nanometer depth resolution is amplitudes in the tens of nanometers at the surface height range, which can be
achieved by using two cameras with optics wafer surface and within λs in the range of measured for a certain configuration;
that image the entire wafer, with the exact this is the limiting surface angle
same field of view, at different conjugation (α lim =atan p⁄d ), which is given by the
planes. Monochromatic incoherent light is
illuminating the wafer and lateral resolution
is determined by the lenses used for a
specific field of view and the number of
pixels offered by the image sensor.
As WFPI is an obvious candidate for
incoming wafers at the front end of line
(FEOL, i.e., the fab process up to when active
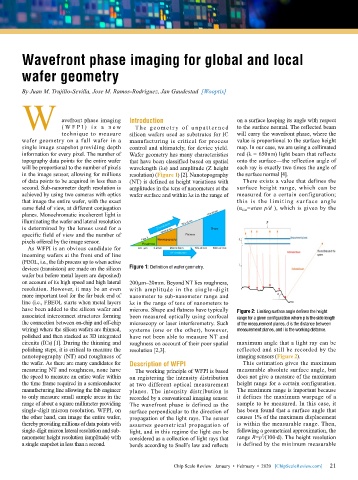
devices (transistors) are made on the silicon Figure 1: Definition of wafer geometry.
wafer but before metal layers are deposited)
on account of its high speed and high lateral 200µm–20mm. Beyond NT lies roughness,
resolution. However, it may be an even with amplitude in the single-digit
more important tool for the far back end of nanometer to sub-nanometer range and
line (i.e., FBEOL starts when metal layers λs in the range of tens of nanometers to
have been added to the silicon wafer and microns. Shape and flatness have typically Figure 2: Limiting surface angle defines the height
associated interconnect structures forming been measured optically using confocal range for a given configuration where p is the side length
the connection between on-chip and off-chip microscopy or laser interferometry. Such of the measurement planes, d is the distance between
wiring) where the silicon wafers are thinned, systems (one or the other), however, measurement planes, and l is the working distance.
polished and then stacked as 3D integrated have not been able to measure NT and
circuits (ICs) [1]. During the thinning and roughness on account of their poor spatial maximum angle that a light ray can be
polishing steps, it is critical to measure the resolution [2,3]. reflected and still be recorded by the
nanotopography (NT) and roughness of imaging sensors (Figure 2).
the wafer. As there are many candidates for Description of WFPI This estimation gives the maximum
measuring NT and roughness, none have The working principle of WFPI is based measurable absolute surface angle, but
the speed to measure an entire wafer within on registering the intensity distribution does not give a measure of the maximum
the time frame required in a semiconductor at two different optical measurement height range for a certain configuration.
manufacturing line allowing the fab engineer planes. The intensity distribution is The maximum range is important because
to only measure small sample areas in the recorded by a conventional imaging sensor. it defines the maximum warpage of a
range of about a square millimeter providing The wavefront phase is defined as the sample to be measured. In this case, it
single-digit micron resolution. WFPI, on surface perpendicular to the direction of has been found that a surface angle that
the other hand, can image the entire wafer, propagation of the light rays. The sensor causes 1% of the maximum displacement
thereby providing millions of data points with assumes geometrical propagation of is within the measurable range. Then,
single-digit micron lateral resolution and sub- light, and in this regime the light can be following a geometrical approximation, the
2
nanometer height resolution (amplitude) with considered as a collection of light rays that range R=p ⁄(100∙d). The height resolution
a single snapshot in less than a second. bends according to Snell’s law and reflects is defined by the minimum measurable

21
Chip Scale Review January • February • 2020 [ChipScaleReview.com] 21